In this post, I want to share how to do preliminary sizing of cyclones.
Cyclone is the most common and effective gas-solids separator that uses centrifugal force. They can be constructed from a variety of materials, are generally simple structures, and can be designed to operate at high temperatures and pressures.
The reverse-flow cyclone is the most common design. In a reverse-flow cyclone, the gas enters the top chamber tangentially, spirals down to the conical section’s apex, and then moves up in a second spiral with a lower diameter before leaving through a central vertical pipe at the top. The solids travel radially to the walls, down the walls, and then are gathered at the bottom.
Cyclone Design
There are two standard designs for gas-solid cyclones, a high-efficiency cyclone and a high throughput cyclone. Standard cyclone dimension of each type is presented in figure below.

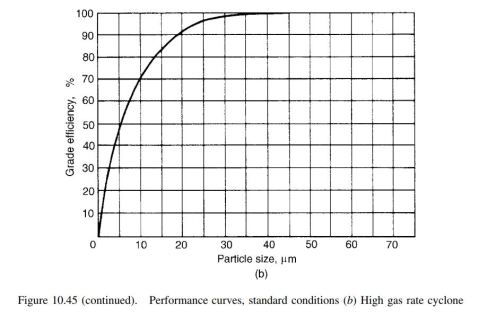
The performance curve of these designs is obtained experimentally under standard test conditions. The performance curve is shown below.

The following scaling equation can be used to adjust these curves to different cyclone sizes and operational settings for a specific separation efficiency:
Where:
d1 = mean diameter of particle separated at standard conditions, at the chosen separating efficiency
d1 = mean diameter of particle separated in the proposed design, at the same separating efficiency
Dc1 = diameter of standard cyclone = 8 in (203 mm)
Dc1 = diameter of proposed cyclone, mm
Q1 = standard flow rate (for high efficiency design = 223 m3/h, for high throughput design = 669 m3/h)
∆ρ1 = solid fluid density difference in standard condition (2000 kg/m3)
∆ρ2 = density difference, proposed design
μ1 = test fluid viscosity (air at 1 atm, 20oC) = 0.018 cP
μ2 = viscosity, proposed fluid
A performance curve for the proposed design can be drawn up by multiplying the grade diameter by scaling factor given by equation above.
The ideal inlet velocity has been determined to be 15 m/s (50 ft/s), although the cyclone should be built to give an inlet velocity of between 9 and 27 m/s (30 to 90 ft/s).
Pressure Drop
The entry and exit losses, friction, and kinetic energy losses within the cyclone all contribute to the pressure drop in the cyclone. To calculate the pressure drop, use the empirical equation below:
Where:
∆P = cyclone pressure drop, millibars
ρf = gas density, kg/m3
u1 = inlet duct velocity, m/s
u2 = exit duct velocity, m/s
rt = radius of circle to which the centre line of the inlet is tangential, m
re = radius of exit pipe, m
Φ = factor from figure below
Ψ = parameter in figure below, given by:
fc = friction factor, taken as 0.005 for gases
As = surface area of cyclone exposed to spinning fluid, m2. For design purpose this can be taken as equal to the surface area of a cylinder with the same diameter as the cylone and length equal to the total height of the cyclone (barrel plus cone).
A1 = area of inlet duct, m2
Pressure drop equation above is for gas flowing alone, containing no solids. Depending on the solids loading, the pressure loss caused by the solids will typically be more than that predicted by equation above.
Based on Perry, pressure drop of cyclone composed of five components, which are pressure drop due to:
- Inlet contraction
- Particle acceleration
- Barrel friction
- Gas flow reversal
- Exit contraction
The total pressure drop is the sum of the five individual pressure drops. Figure below gives the actual pressure drop based on the loading.

Let’s see example below.
Example
Design a cyclone to recover solids from a process gas stream. The anticipated particle size distribution in the inlet gas is given below. The density of the particles is 2500 kg/m3, and the gas is essentially nitrogen at 150oC. The stream volumetric flowrate is 4000 m3/h, and the operation is at atmospheric pressure. An 80% recovery of the solids is required.
| Particle size (μm) | 50 | 40 | 30 | 20 | 10 | 5 | 2 |
| Percentage by weight less than | 90 | 75 | 65 | 55 | 30 | 10 | 4 |
Solution
To determine which type of cyclone is suitable, let’s see the percentage of particles below 10 μm. As 30% of the particles are below 10 μm, the high-efficiency design will be required to give the specified recovery.
Why 10 μm?
Based on Perry, field of application of cyclone is for 5-10 micron.
Flow rate = 4000 m3/h = 1.11 m3/s
Area of inlet duct at 15 m/s = 1.11 /15 = 0.07 m2
For high-efficiency cyclone, area of inlet duct = 0.5 Dc × 0.2 Dc = 0.7 m2
Dc = [0.07/(0.5 × 0.2)]0.5 = 0.84 m
Diameter of standard cyclone is 0.203 m, so the above design is too large compared to standard.
Try four cyclones in parallel, then:
Dc = [0.07/(0.5 × 0.2 × 4)]0.5 = 0.42 m
Flowrate per cyclone = 4000 / 4 = 1000 m3/h
Density of gas N2 at 150oC = 28 /22.4 × 273 (273 + 150) = 0.81 kg/m3
The density of solid is 2500 kg/m3, so density of gas is negligible.
Viscosity of N2 at 150oC = 0.023 cP
Scaling factor:
The performance calculations using the scaling factor are set out in table below:
The performance curve after scaling is depicted in figure below (green line):

The collection efficiencies shown in column 4 of the table were read at the scaled particle size, column 3. The overall collection efficiency satisfies the specified solids recovery. The proposed design with dimension in the proportions given in figure below.
Pressure Drop Calculation
Area of inlet duct, A1 = 210 × 84 = 17,640 mm2
Cyclone surface area = Π (420) × (630 + 1050) = 2,216,708 mm2
fc , friction factor, taken as 0.005 for gases,
Ψ = fc × As/A1 = 0.005 × 2,216,708 / 17,640 = 0.63
rt/re = (420 – (84/2)) / 210 = 1.8
Based on figure, we get Φ = 0.9
Inlet duct velocity, u1, is calculated:
u1 = 1000 / 3600 × 1,000,000/17,640 = 15.75 m/s
Area of exit pipe = Π × 210 × 210 / 4 = 34,636 mm2
u2 = 1000 / 3600 × 1,000,000/34,636 = 8.0 m/s
From equation,
∆P = 5.67 millibar
Reference:
- Coulson and Richardson’s Chemical Engineering Volume 6
- Perry Chemical Engineer’s Handbook Ed 8








